Anteilige Energieeinsparung
In Großanlagentypen zur Trinkwarmwasserversorgung mit und ohne Heizungsunterstützung wird die Anteilige Energieeinsparung nach DIN CEN/TS 12977-2 im Projektbericht ausgegeben.
Anteilige Energieeinsparung = ($Q_{\text{conv}}$ - $Q_{\text{aux}}$) / $Q_{\text{conv}}$
$Q_{\text{conv}}$ ist der Energieaufwand einer konventionellen Vergleichsanlage. (Begriff in der Norm: “Bruttoenergiebedarf der Referenzanlage”)
$Q_{\text{aux}}$ ist der konventionelle Energieaufwand der simulierten Solaranlage, also die Energie, die die Nachheizung in das System liefert. In der Norm steht: “$Q_{\text{aux}}$ ist der Bruttozusatzenergiebedarf der solaren Heizungsanlage, um den erforderlichen Wärmebedarf zu decken.” Dabei wird derselbe Kesselwirkungsgrad angenommen wie bei der konventionellen Anlage.
Bei der Ermittlung von $Q_{\text{conv}}$ werden Zirkulationsverluste berücksichtigt. Durch die Berücksichtigung der Zirkulation hier in der Simulation (Parameter > Warmwasserverbrauch > Zirkulation vorhanden) wird $Q_{\text{aux}}$ größer, weil die Nachheizung mehr Energie in das System liefert, als es ohne Zirkulation der Fall gewesen wäre.
Die Anteilige Energieeinsparung ist gleich 1 bzw. 100%, wenn der Zusatzenergiebedarf $Q_{\text{aux}}$ gleich 0 ist. Dann wurde die gesamte Energie von der Solaranlage geliefert, die Nachheizung lief zu keinem Zeitpunkt.
Die Anteilige Energieeinsparung wird negativ, wenn der Zusatzenergiebedarf $Q_{\text{aux}}$ größer ist als $Q_{\text{conv}}$.
Außerdem gilt:
$ Q_{\text{conv}} = \frac{Q_{\text{conv.net}}}{\eta_{\text{conv}}}, $
mit
$ \eta_{\text{conv}} = $ Wirkungsgrad der Vergleichsanlage
$ Q_{\text{conv.net}} = $ Netto-Energiebedarf in [Wh]
$ Q_{\text{conv.net}} = Q_{\text{Hzg}} + Q_{\text{ww}} + Q_{\text{sp.conv}}, $ and
$ Q_{\text{Hzg}} = $ Energiebedarf für die Heizung
$ Q_{\text{ww}} = $ Energiebedarf für Warmwasser
$ Q_{\text{Sp conv}} = $ Energiebedarf für den Speicher $= 0,16 \times \sqrt{\text{Speichervolumen}} \times \Delta T \times \text{Betriebsstunden} $
The Temperaturdifferenz ΔT ergibt sich aus der Differenz der Speichertemperatur und der Umgebungstemperatur des Speichers. Sie beträgt i.d.R. 30 K.
Verbesserte Berechnung von Schwimmbädern
In T*SOL werden auch Schwimmbadsysteme (Frei- und Hallenbäder) simuliert. In der Praxis werden immer mehr konventionelle Schwimmbadheizungsanlagen durch Solaranlagen ergänzt. T*SOL unterstützt den Planer dabei, die Energieeinsparung solcher Kombinationen zu berechnen.
Das bisherige Schwimmbad-Simulationsmodell von T*SOL wurde grundsätzlich überarbeitet und verbessert:
- Unterscheidung zwischen privaten und öffentlichen Bädern
- Berücksichtigung von (stündlich) vorgebbaren Nutzungszeiten durch Badegäste
- Berücksichtigung von eventuellen Verschattungsanteilen der Wasserfläche
- Neue Algorithmen zur Berechnung der Einstrahlungsgewinne mit Unterscheidung zwischen diffusen und direkten Strahlungsanteilen
- Genauere Erfassung des Bewölkungseinflusses
- Neue Algorithmen zur Berechnung der Verdunstung und der Konvektion
- Neues thermodynamisches Modell der Abdeckung
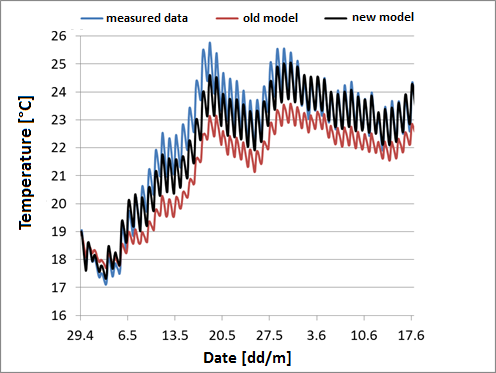
Die verbesserten Algorithmen wurden mit Hilfe von Messdaten [1] validiert (vgl. Abb. 1).
Abb. 1 Verlauf der Mess- und Simulationswerte der Beckentemperatur (54 Tage) Temperaturverlauf, Messwerte, bisheriges Modell, neues Modell
Wie in Abb. 1 zu sehen ist, konnte eine deutliche Steigerung der Simulationsqualität erreicht werden. Mit einem RMSD [2] von 0,48 °C liegt das neue Modell deutlich unter den 1,38 °C des bisherigen Modells.
Simulationsmodell
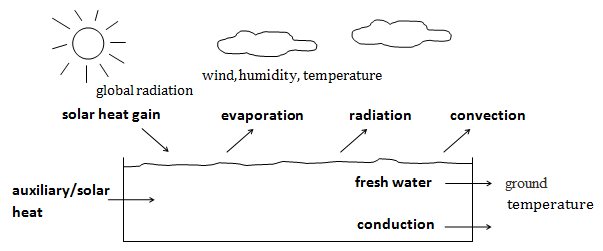
Die mittlere Beckenwassertemperatur wird aus den Klimadaten des Standorts, den Betriebsparametern und den Umgebungsbedingungen ermittelt. Dazu werden die auftretenden Wärmetransportströme berechnet (vgl. Abb. 2).
Abb. 2 Energiebilanz des Schwimmbeckens Globalstrahlung, Wind, Luftfeuchte, Außentemperatur, Strahlungsabsorption, Verdunstung, Strahlungsverluste, Konvektion, Energiezufuhr durch Heizung oder Solaranlage, Frischwasserverluste, Wärmeleitung, Bodentemperatur
Die Berechnung der einzelnen Wärmetransportmechanismen wurde auf Basis aktueller Veröffentlichungen zur Schwimmbadthematik überarbeitet. Eine detaillierte Beschreibung finden Sie hier: http://www.valentin-software.com/sites/default/files/tagungsband_schiwmmbad_-usb.pdf
Durch Bilanzierung der Wärmeströme Q ̇_i wird mit einer zeitlichen Auflösung von bis zu 6 Minuten der zeitliche Verlauf der Beckenwassertemperatur T_w(t) berechnet. Im Modell wird dabei davon ausgegangen, dass die Temperatur im gesamten Becken konstant ist (Ein-Knoten-Modell):
(dT_w)/dt = (∑▒Q ̇_i) / (c_pw∙ρ_w∙V_w)
T_w: Temperatur des Wassers in K Q_i: Wärmetransportgrößen in J c_pw: spezifische Wärmekapazität von Wasser in J/(kg K) ρ_w: Dichte des Wassers in kg/m³ V_w: Volumen des Beckens in m³
Beispiele von Simulationsergebnissen
Die einzelnen Energietransportmechanismen und Zustandsgrößen lassen sich in Programme wie Excel übertragen oder auch direkt im T*SOL grafisch ausgeben:
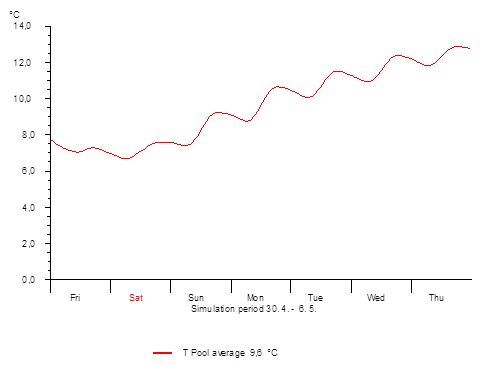
Abb. 3 Verlauf der Wassertemperatur eines frisch gefüllten Beckens in der ersten Maiwoche (T*SOL-Diagramm)
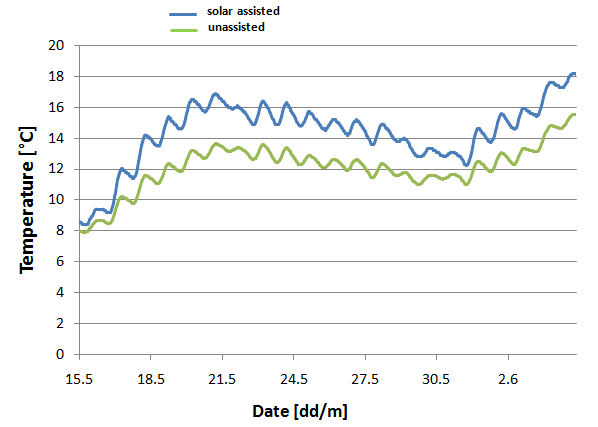
Abb. 4 Verlauf der Wassertemperatur eines frisch gefüllten Beckens mit und ohne Solaranlage, Mitte Mai bis Anfang Juni (EXCEL Grafik)
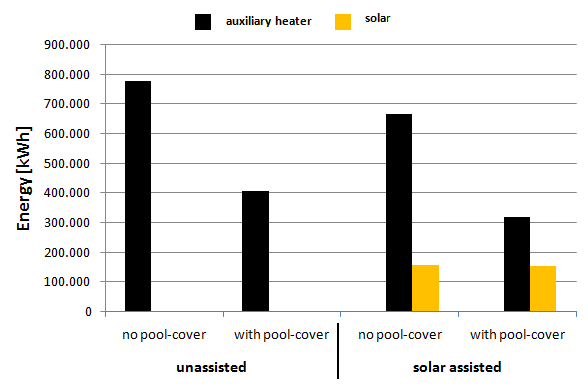
Energieeffizienzmaßnahmen, wie z.B. die Verwendung einer Abdeckung oder die Auslegung einer Solaranlage können durch eine Gegenüberstellung von Simulationsergebnissen analysiert werden. In Abb. 5 sind die Heizenergiebedarfe und solaren Energiebeiträge eines fiktiven öffentlichen Beckens bei verschiedenen Systemkonfigurationen dargestellt.
Abb. 5 Heizenergiebedarfe und solare Energiebeiträge für verschiedene Systemvarianten eines fiktiven öffentlichen Beckens bei einer Wasser-Solltemperatur von 23 °C
Man erkennt, dass alleine die Verwendung einer Abdeckung den Energiebedarf deutlich senkt. In diesem Beispiel liegt die Einsparung bei ca. 47%. Der Effekt einer Abdeckung variiert mit den klimatischen Verhältnissen und den Abdeckzeiten. Die Solaranlage leistet zur Abdeckung in diesem Beispiel zusätzliche Einsparungen von ca. 21%.
Ein weiterer Effekt besteht darin, dass bei Nutzung einer Solaranlage und gleichzeitiger Verwendung einer Abdeckung, die durchschnittliche Schwimmbadtemperatur im obigen Beispiel von der vorgegebenen Solltemperatur von 23 °C auf 24 °C ansteigt. Hier könnte man nun Überlegungen anstellen, ob die Temperaturerhöhung gewünscht ist oder evtl. aus ökonomischen Gründen eine kleinere Anlage besser geeignet ist.
Je nach Standort und Nutzungsparametern können die klimatischen Unterschiede die Ergebnisse deutlich beeinflussen. Mit dem überarbeiteten Simulationsmodell kann die aus den Umgebungsbedingungen resultierende Dynamik wesentlich besser als bisher abgebildet werden und die Simulation kann als ein nützliches Tool bei energetischen Fragestellungen rund um die Schwimmbadthematik dienen.
[1] Datengrundlage: Woolley, J., Harrington, C., Modera, M.: Swimming pools as heat sinks for air conditioners: Model design and experimental validation for natural thermal behavior of the pool. In: Building and Environment (2011), Vol. 46, S. 187-195
[2] Engl. Root Mean Square Deviation, ein statistisches Maß für die Streuung von Berechnungswerten um Messwerte
Wirtschaftlichkeitsberechnung
Die Wirtschaftlichkeitsberechnung in T*SOL nach der Barwertmethode beruht auf folgenden Formeln:
Investitionskosten = Anlagenkosten - Förderung
Jährliche Betriebskosten = Pumpenleistung * Laufzeit * Stromkosten
Der Barwert einer preisdynamischen Zahlungsfolge Z, Zr, Zr², … über T Jahre (Lebensdauer) nach VDI 2067 ist:
$NPV = Z * b(T, q, r) $
$b(T,q,r) = \begin{cases} \frac{1 - \left(\frac{r}{q}\right)^T}{q - r} & \text{if } r \neq q, \\ \frac{T}{q} & \text{if } r = q \end{cases}$
q: Kapitalzinsfaktor (z. B. 1,08 bei 8% Kapitalzins)
r: Preisänderungsfaktor (z. B. 1,1 bei 10% Preisänderung)
Für den Kapitalwert der Gesamtinvestition gilt:
$ K = \sum[\text{BW der preisdynamischen Zahlungsfolge über die Lebensdauer}] - \text{Investitionen} + \text{Förderungen} $
Die Amortisationszeit ist der Zeitraum, den die Anlage laufen muss, um für die Investition einen Barwert von Null zu erbringen. Amortisationszeiten größer als 40 Jahre werden nicht angezeigt.
Für die Berechnung des Wärmepreises wird der Barwert der Kosten ermittelt:
$ \text{Barwert der Kosten BW} = \text{Investition} + \text{BW der Betriebs- und Wartungskosten} $
Wandelt man den BW der Kosten in eine konstante Zahlungsfolge ($ r = 1 $) über die Lebensdauer um, so gilt für diese Folge $ Z $:
$ Z = \frac{\text{BW der Kosten}}{b(T, q, r)} $
Für $ r = 1 $ wird $ \frac{1}{b(T, q, r)} $ zum Annuitätsfaktor:
$ a(q, t) = \frac{q^T \cdot (q - 1)}{q^T - 1} $ (ebenfalls nach VDI 2067)
Der Wärmepreis ist dann:
$ \text{Wärmepreis} = \frac{\text{Jährliche Kosten Z}}{\text{Jahresenergieertrag}} $