Enhanced Calculation of Swimming Pools
In T*SOL®, swimming pool systems (indoor and outdoor) are now simulated. In practice, conventional swimming pool heating systems are increasingly complemented by solar installations. T*SOL® assists planners in calculating the energy savings of such combinations.
The existing swimming pool simulation model in T*SOL® has been fundamentally revised and improved:
- Differentiation between private and public pools
- Consideration of (hourly) presettable usage times by bathers
- Consideration of potential shading portions of the water surface
- New algorithms for calculating radiation gains, distinguishing between diffuse and direct radiation components
- More accurate capture of cloud influence
- New algorithms for calculating evaporation and convection
- New thermodynamic model for covers
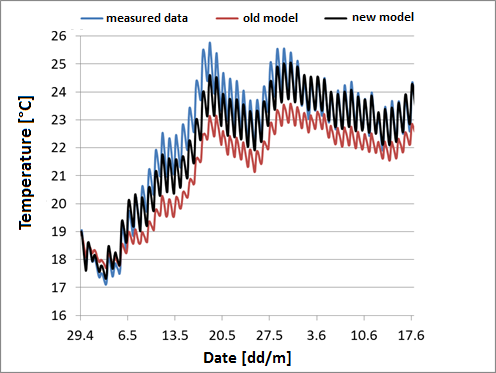
The improved algorithms have been validated using measurement data [^1] (see Fig. 1).
Fig. 1 Comparison of measured and simulated values of pool temperature (54 days) Temperature profile, measured values, previous model, new model
As shown in Fig. 1, a significant increase in simulation quality has been achieved. With an RMSD [^2] of 0.48 °C, the new model is well below the 1.38 °C of the previous model.
Simulation Model
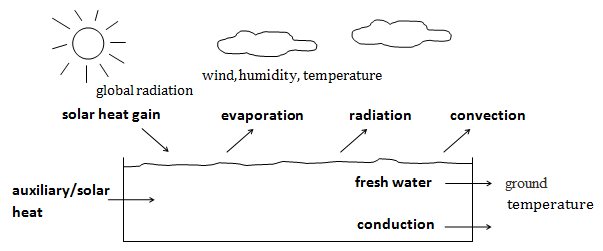
The average pool water temperature is determined from local climate data, operational parameters, and environmental conditions. The occurring heat transport flows are calculated (see Fig. 2).
Fig. 2 Energy balance of the swimming pool
Global radiation, wind, humidity, outside temperature, radiation absorption, evaporation, radiation losses, convection, energy supply by heating or solar system, fresh water losses, heat conduction, ground temperature
The calculation of the individual heat transport mechanisms has been revised based on current publications on swimming pool topics. A detailed description can be found here: http://www.valentin-software.com/sites/default/files/tagungsband_schiwmmbad_-usb.pdf
By balancing the heat flows Q ̇_i, the temporal course of the pool water temperature T_w(t) is calculated with a temporal resolution of up to 6 minutes. The model assumes that the temperature is constant throughout the pool (single-node model):
[\frac{dT_w}{dt} = \frac{\sum Q ̇_i}{c_pw \cdot ρ_w \cdot V_w}]
Where:
- (T_w): Temperature of the water in K
- (Q_i): Heat transport quantities in J
- (c_pw): Specific heat capacity of water in J/(kg K)
- (ρ_w): Density of water in kg/m³
- (V_w): Volume of the pool in m³
Examples of Simulation Results
The individual energy transport mechanisms and state variables can be transferred to programs like Excel or directly visualized in T*SOL®:
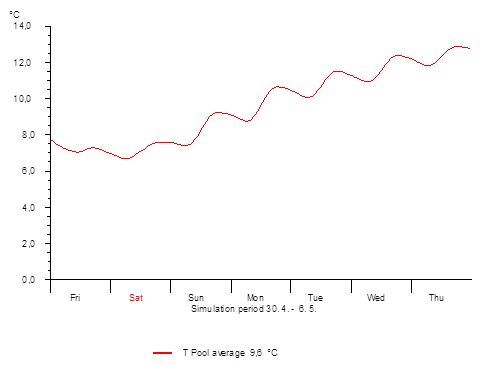
Fig. 3 Temporal profile of the water temperature in a freshly filled pool in the first week of May (T*SOL® diagram)
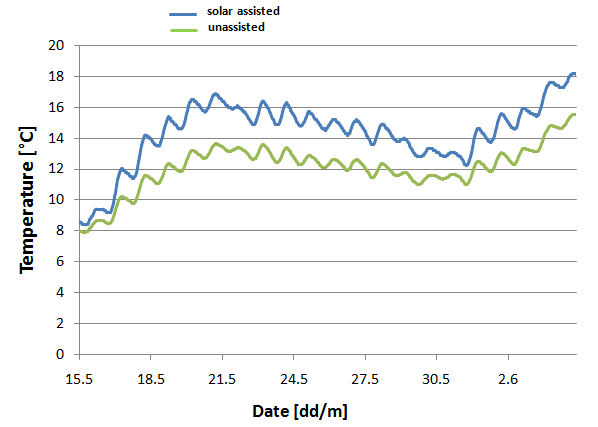
Fig. 4 Temporal profile of the water temperature in a freshly filled pool with and without a solar system, mid-May to early June (EXCEL graph)
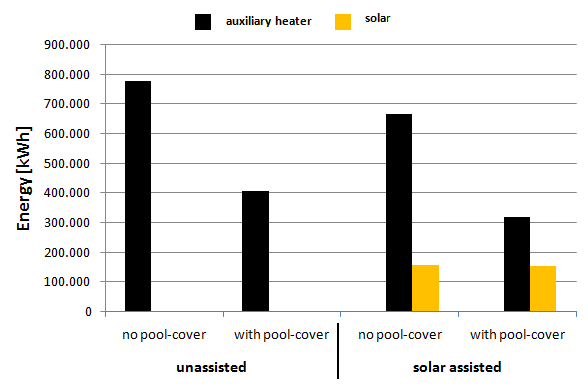
Energy efficiency measures, such as using a cover or designing a solar system, can be analyzed by comparing simulation results. In Fig. 5, the heating energy requirements and solar energy contributions of a fictional public pool with different system configurations are displayed.
Fig. 5 Heating energy requirements and solar energy contributions for different system variants of a fictional public pool with a water target temperature of 23 °C
It is evident that the use of a cover alone significantly reduces energy requirements. In this example, the savings are approximately 47%. The impact of a cover varies with climatic conditions and cover times. In this example, the solar system contributes additional savings of about 21%.
Another effect is that, when using a solar system and simultaneously using a cover, the average pool temperature in the example above increases from the specified target temperature of 23 °C to 24 °C. This raises considerations about whether the temperature increase is desired or if, for economic reasons, a smaller system would be more suitable.
Depending on the location and usage parameters, climatic differences can significantly influence the results. With the revised simulation model, the dynamics resulting from environmental conditions can be better represented than before, making the simulation a valuable tool for energy-related questions regarding swimming pools.
[1] Data source: Woolley, J., Harrington, C., Modera, M.: Swimming pools as heat sinks for air conditioners: Model design and experimental validation for natural thermal behavior of the pool. In: Building and Environment (2011), Vol. 46, pp. 187-195
[2] Root Mean Square Deviation, a statistical measure of the spread of calculated values around measured values