Proportionate Energy Savings
In large-scale systems for domestic hot water supply with and without heating support, the Proportionate Energy Savings, according to DIN CEN/TS 12977-2, are presented in the project report.
Proportionate Energy Savings = ($Q_{\text{conv}}$ - $Q_{\text{aux}}$) / $Q_{\text{conv}}$
$Q_{\text{conv}}$ represents the energy consumption of a conventional reference system. (Term in the standard: “Gross energy requirement of the reference system”)
$Q_{\text{aux}}$ is the conventional energy consumption of the simulated solar system, i.e., the energy supplied to the system by auxiliary heating. The standard states: “$Q_{\text{aux}}$ is the gross additional energy requirement of the solar heating system to meet the required heating demand.” The same boiler efficiency as in the conventional system is assumed.
When calculating $Q_{\text{conv}}$, circulation losses are taken into account. Considering circulation in the simulation (Parameters > Hot Water Consumption > Circulation present), $Q_{\text{aux}}$ becomes larger because the auxiliary heating supplies more energy to the system than it would without circulation.
The Proportionate Energy Savings are equal to 1 or 100% when the additional energy requirement $Q_{\text{aux}}$ is equal to 0. In this scenario, all energy was provided by the solar system, and auxiliary heating was inactive throughout.
The Proportionate Energy Savings turn negative when the additional energy requirement $Q_{\text{aux}}$ exceeds $Q_{\text{conv}}$.
Additionally, the following holds:
$ Q_{\text{conv}} = \frac{Q_{\text{conv.net}}}{\eta_{\text{conv}}}, $ where
$ \eta_{\text{conv}} = $ efficiency of the reference system,
$ Q_{\text{conv.net}} = $ net energy requirement in [Wh].
$ Q_{\text{conv.net}} = Q_{\text{Hzg}} + Q_{\text{ww}} + Q_{\text{sp.conv}}, $ and
$ Q_{\text{Hzg}} = $ energy requirement for heating,
$ Q_{\text{ww}} = $ energy requirement for hot water,
$ Q_{\text{Sp conv}} = $ energy requirement for the storage tank $= 0.16 \times \sqrt{\text{Storage volume}} \times \Delta T \times \text{Operating hours} $.
The temperature difference ΔT is derived from the difference between the storage tank temperature and the ambient temperature of the tank, typically amounting to 30 K.
Enhanced Calculation of Swimming Pools
In T*SOL, swimming pool systems (indoor and outdoor) are now simulated. In practice, conventional swimming pool heating systems are increasingly complemented by solar installations. T*SOL assists planners in calculating the energy savings of such combinations.
The existing swimming pool simulation model in T*SOL has been fundamentally revised and improved:
- Differentiation between private and public pools
- Consideration of (hourly) presettable usage times by bathers
- Consideration of potential shading portions of the water surface
- New algorithms for calculating radiation gains, distinguishing between diffuse and direct radiation components
- More accurate capture of cloud influence
- New algorithms for calculating evaporation and convection
- New thermodynamic model for covers
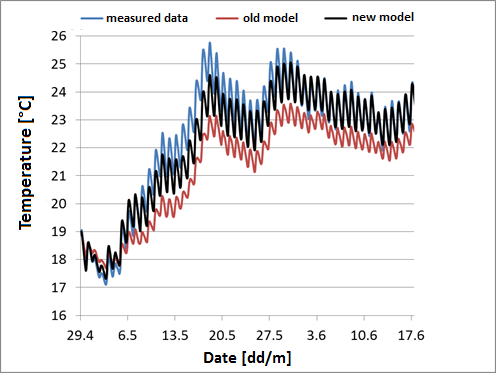
The improved algorithms have been validated using measurement data [^1] (see Fig. 1).
Fig. 1 Comparison of measured and simulated values of pool temperature (54 days) Temperature profile, measured values, previous model, new model
As shown in Fig. 1, a significant increase in simulation quality has been achieved. With an RMSD [^2] of 0.48 °C, the new model is well below the 1.38 °C of the previous model.
Simulation Model
The average pool water temperature is determined from local climate data, operational parameters, and environmental conditions. The occurring heat transport flows are calculated (see Fig. 2).
Fig. 2 Energy balance of the swimming pool
Global radiation, wind, humidity, outside temperature, radiation absorption, evaporation, radiation losses, convection, energy supply by heating or solar system, fresh water losses, heat conduction, ground temperature
The calculation of the individual heat transport mechanisms has been revised based on current publications on swimming pool topics. A detailed description can be found here: http://www.valentin-software.com/sites/default/files/tagungsband_schiwmmbad_-usb.pdf
By balancing the heat flows Q ̇_i, the temporal course of the pool water temperature T_w(t) is calculated with a temporal resolution of up to 6 minutes. The model assumes that the temperature is constant throughout the pool (single-node model):
[\frac{dT_w}{dt} = \frac{\sum Q ̇_i}{c_pw \cdot ρ_w \cdot V_w}]
Where:
- (T_w): Temperature of the water in K
- (Q_i): Heat transport quantities in J
- (c_pw): Specific heat capacity of water in J/(kg K)
- (ρ_w): Density of water in kg/m³
- (V_w): Volume of the pool in m³
Examples of Simulation Results
The individual energy transport mechanisms and state variables can be transferred to programs like Excel or directly visualized in T*SOL:
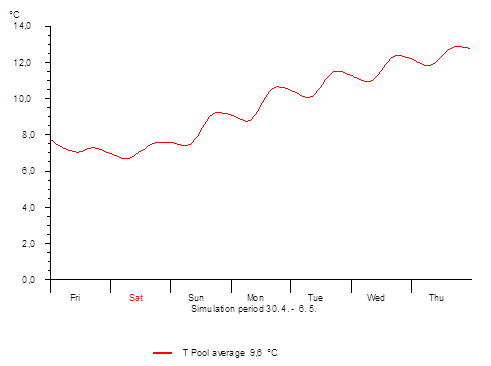
Fig. 3 Temporal profile of the water temperature in a freshly filled pool in the first week of May (T*SOL diagram)
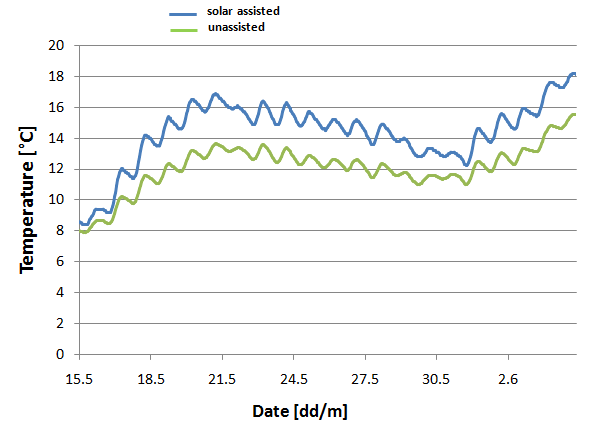
Fig. 4 Temporal profile of the water temperature in a freshly filled pool with and without a solar system, mid-May to early June (EXCEL graph)
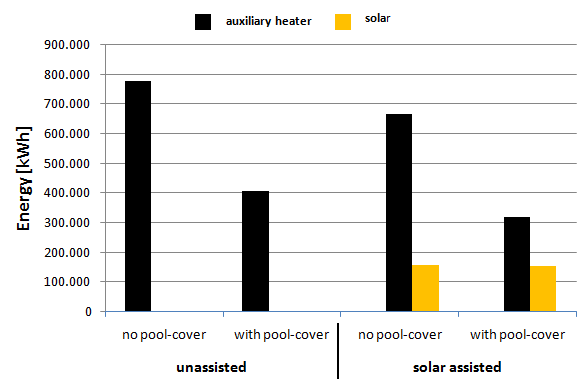
Energy efficiency measures, such as using a cover or designing a solar system, can be analyzed by comparing simulation results. In Fig. 5, the heating energy requirements and solar energy contributions of a fictional public pool with different system configurations are displayed.
Fig. 5 Heating energy requirements and solar energy contributions for different system variants of a fictional public pool with a water target temperature of 23 °C
It is evident that the use of a cover alone significantly reduces energy requirements. In this example, the savings are approximately 47%. The impact of a cover varies with climatic conditions and cover times. In this example, the solar system contributes additional savings of about 21%.
Another effect is that, when using a solar system and simultaneously using a cover, the average pool temperature in the example above increases from the specified target temperature of 23 °C to 24 °C. This raises considerations about whether the temperature increase is desired or if, for economic reasons, a smaller system would be more suitable.
Depending on the location and usage parameters, climatic differences can significantly influence the results. With the revised simulation model, the dynamics resulting from environmental conditions can be better represented than before, making the simulation a valuable tool for energy-related questions regarding swimming pools.
[1] Data source: Woolley, J., Harrington, C., Modera, M.: Swimming pools as heat sinks for air conditioners: Model design and experimental validation for natural thermal behavior of the pool. In: Building and Environment (2011), Vol. 46, pp. 187-195
[2] Root Mean Square Deviation, a statistical measure of the spread of calculated values around measured values
Economic Calculation
The economic calculation in T*SOL using the net present value method is based on the following formulas:
Investment Costs = Installation Costs - Subsidy
Yearly Operating Costs = Pump Performance * Operating Time * Electricity Costs
The Net Present Value (NPV) of a price-dynamic payment sequence Z, Zr, Zr², … over T years (lifespan) according to VDI 2067 is:
$ NPV = Z * b(T, q, r) $
$b(T,q,r) = \begin{cases} \frac{1 - \left(\frac{r}{q}\right)^T}{q - r} & \text{if } r \neq q, \\ \frac{T}{q} & \text{if } r = q \end{cases}$
- q: Capital interest factor (e.g., 1.08 for 8% capital interest)
- r: Price change factor (e.g., 1.1 for 10% price change)
For the Capital Value (CV) of the total investment:
$K = \sum[\text{NPV of the price-dynamic payment sequence over the lifespan}] - \text{Investments} + \text{Subsidies}$
The payback period is the time the system must operate to yield a net present value of zero. Payback periods exceeding 40 years are not displayed.
To calculate the heating price, the net present value of the costs is determined:
$\text{NPV of Costs (BW)} = \text{Investments} + \text{NPV of Operating and Maintenance Costs}$
If the NPV of the costs is converted into a constant payment sequence ($r = 1$), then the following applies to this sequence $Z$:
$Z = \frac{\text{NPV of Costs}}{b(T, q, r)}$
For $r = 1$, $\frac{1}{b(T, q, r)}$ becomes the annuity factor:
$a(q, T) = \frac{q^T \cdot (q - 1)}{q^T - 1}$ (also according to VDI 2067)
The Heating Price is then:
$\text{Heating Price} = \frac{\text{Yearly Costs Z}}{\text{Yearly Energy Yield}}$