Bleibatterien

Es gibt in der Literatur bereits eine Vielzahl von sehr guten Modellen für Bleisäure-Akkumulatoren, die je nach Anwendungszweck variieren. Problematisch ist, bei diesen in der Regel auf elektrischen Ersatzschaltbildern (ESB) beruhenden Modellen, die Parametrisierung für beliebige Batterie-Typen. Da die Schnittmenge aus bestehenden Modellen und der Anforderungsanalyse für unser Simulationsmodell zu gering war, wurde ein eigenes Modell entwickelt, das Teile der ESB mit empirischen Elementen verbindet.

Die wesentlichen Anforderungen, denen unser Modell genügt, sind die folgenden:

  • Die Spannungen werden präzise abgebildet (Unterschied Entladen und Laden, Innenwiderstand, Kristallisation)
  • Die Kennlinien der Entlade- und Ladevorgänge sind möglichst realistisch
  • Selbstentladung wird berücksichtigt
  • Die normative Zyklenbelastung und Lebensdauer geht in die Simulation ein

Um die Eigenheiten einer spezifischen Batterie abbilden zu können, benötigt das Modell folgende Parameter vom Datenblatt:

  • Kapazität in Abhängigkeit der Entladezeit
  • Innenwiderstand
  • Bauart (verschlossen, geschlossen, Gel, etc.)
  • Maximale Entladetiefe (i.d.R. 80 %) und maximaler Entladestrom
  • Selbstentladungsrate
  • Zyklenzahl über Entladetiefe

Entladen

Für das Entladen ist die Berechnung des Kennlinienfelds essentiell. Bleibatterien zeigen bei der Entladung mit konstantem Strom eine Charakteristik mit stetig abfallender Spannung. Je höher dabei der Entladestrom ist, desto stärker der Spannungsabfall. Abbildung 1 zeigt das modellierte Entladeprofil für eine 600 Ah-Zelle, die mit variierender Leistung belastet wird.

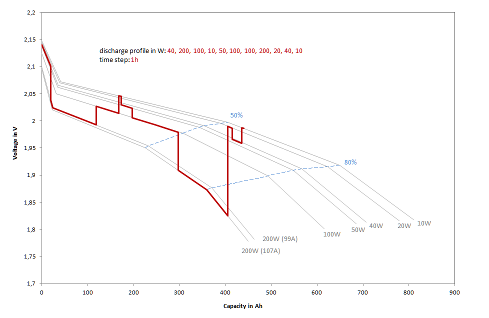
Abbildung 1: Typische Entladeprofile (W) (Spannung über Kapazität) für eine 600 Ah-Zelle mit Zeitschritt = 1 Stunde

Für die Simulation muss also für jeden Entladestrom zunächst die Kennlinie aus Spannungen und Kapazitäten berechnet werden. Dabei spielen die Bauart der Batterie, ihr Innenwiderstand und die Kapazitätscharakteristik die entscheidenden Rollen. Soll das Entladen mit konstanter Leistung erfolgen, muss der Entladestrom iterativ angenähert werden, um über das Integral der Spannungsänderung und dem Strom die gewünschte Leistung während des Zeitschrittes zu erhalten. Weiterhin zu beachten ist die durch die maximale Entladetiefe gegebene Entladeschlussspannung. Zur Schonung der Batterien dürfen diese in der Regel nicht zu mehr als 80% entladen werden. Da sich die der Batterie entnehmbare Gesamtkapazität mit dem Entladestrom ändert, ist auch die Entladeschlussspannung vom Strom abhängig, wie aus Abbildung 1 hervorgeht.

Der State of Function stellt sicher, dass vor Entladen einer bestimmten Energiemenge geprüft wird, ob nach dem Entladen mit dem resultierenden Strom die maximale Entladetiefe unterschritten wird, und weist gegebenenfalls die Entladung zurück.

Laden

Das Laden einer Batterie kann nach unterschiedlichen Ladeprofilen erfolgen, in diesem Fall wird mit einem IU0U-Profil geladen.

Zunächst wird mit konstantem Strom geladen (I-Ladung oder Bulk-Phase), während die Spannung in der Zelle steigt. Ist eine definierte Spannung erreicht, erfolgt eine zeitgesteuerte Phase mit konstanter Spannung, wobei Zeitdauer und Ladespannung variieren können.

  • Boost-Ladung (U0): 2 h bei 2,4 bis 2,45 V
  • Voll-Ladung: 5 h bei 2,4 V
  • Ausgleichs-Ladung: 10 h bei 2,4 V

Im Anschluss, also nach der festgelegten Zeitdauer, wird in der Erhaltungs-Phase (Float-Ladung) die Spannung auf 2,23 bis 2,3V heruntergesetzt, um ein Überladen zu vermeiden. Wie hoch die so genannte Ladeerhaltungsspannung sein muss, wird dem Datenblatt der Batterie entnommen.

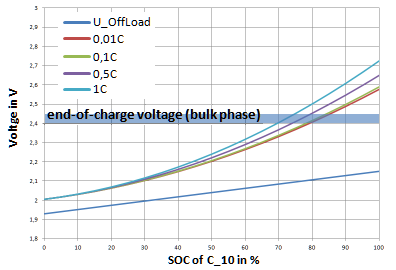
Während der Bulkphase wird üblicherweise so lange mit konstantem Strom geladen, bis die Zellspannung den voreingestellten Wert erreicht. In der Literatur ist leider kein formeller Zusammenhang zwischen Ladestrom, SOC und sich einstellender Spannung in der Bulkphase zu finden.

Daher wurden die in diversen Quellen dargestellten Lade-Diagramme ausgewertet und daraus eine Formel zur Bestimmung der Ladespannung in Abhängigkeit des Stromes (xC als C-Rate) und des SOC entwickelt.

$$ U_B (SOC, xC) = U_R (SOC) + U_K + SOC^2 (0.35 + 0.15 xC) $$

  • $U_B$ - Bulkspannung
  • $U_R$ -Ruhespannung
  • $U_K$ -Spannungsfall durch Kristallisation

Abbildung 2: Abhängigkeit der Zellspannung vom Ladestrom und SOC10 für verschiedene Ladeströme

Je höher also der Entladestrom, desto eher wird die Spannungsgrenze zur nächsten Phase erreicht – desto niedriger ist jedoch auch der SOC bei dieser Spannung. Aus den unterschiedlichen Spannungsniveaus zwischen Laden und Entladen lässt sich weiterhin auch der Ah-Wirkungsgrad einer Zelle im Betrieb berechnen.

Zyklen, Lebensdauer

Auf den Datenblättern angegeben wird die nach Norm (DIN EN 60896) gemessene Anzahl von Zyklen von Entlade- und Ladevorgängen, nach denen die noch entnehmbare C3-Kapazität bis zu einer Ladeschlussspannung von 1,7 V noch 80 % der Bemessungskapazität (laut Norm auch C3) beträgt.

Nach Norm für verschlossene Zellen wird in den Zyklen mit Strömen von 2 I10 2h lang entladen, was einer Entladetiefe von DOD = 40 % bezogen auf C10 entspricht. Bei geschlossenen Zellen sind es 3h mit 2 I10, weswegen man hier eine Entladetiefe von DOD = 60 % erreicht.

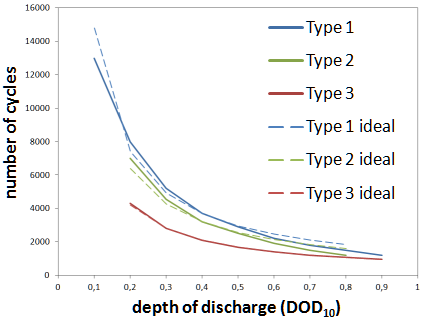
Das Diagramm „Zyklenzahl über Entladetiefe“, das sich auf vielen Datenblättern findet (siehe unten aus Datenblättern von drei verschiedenen Herstellern), extrapoliert dieses eine, nach Norm gemessene Wertepaar immer etwa nach dem Zusammenhang „halbe Entladetiefe – doppelte Zyklenzahl“. Dieser ideale Zusammenhang ist mit gestrichelten Linien dargestellt.

Abbildung 3: Zusammenhang zwischen Entladetiefe und Zyklenzahl verschiedener Batterien

In der Praxis wirkt sich eine tiefer gehende Zyklisierung in der Regel aber stärker auf den Kapazitätsverlust aus als eine flache, weswegen die angegebenen Kurven von der Idealform abweichen. Dies kann mit Korrekturfaktoren berücksichtigt werden, die je nach Batterie-Baureihe und Hersteller variieren.

Während der gesamten Simulation wird (nur im Falle des Entladens) eine Amperestunden-Bilanz gebildet, wobei bei jedem Zeitschritt die aktuell entnommene Kapazität, gewichtet mit den Korrekturfaktoren für die Zyklenbelastung $f_\text{Ah}$ aus obenstehender Grafik, hinzuaddiert wird.

Diese Ah-Bilanz kann mit der nach Norm gemessenen Gesamtzyklenzahl ins Verhältnis gesetzt werden und geht dann in die Berechnung des Kapazitätsrückgangs ein, so dass nach Erreichen der Gesamtzyklenzahl die Nennkapazität auf 80 % gesunken ist:

$$ C_{\text{N}} (C_{\text{Ah}}) = C_{\text{N,0}} (1- 0.2 \zeta ) $$

mit der Zyklenbelastung

$$ \zeta = \frac{\sum ^{\text{now}}_{i=0} \left( f_{\text{Ah,i}}(DOD_{10}) I_i t_i \right) }{C_{\text{Ah,N}}} $$

  • $C_{\text{N}}$ : Nennkapazität
  • $C_{\text{N,0}}$ : Nennkapazität zu Beginn der Nutzung
  • $C_{\text{Ah}}$ : bilanzierte Ah-Kapazität
  • $C_{\text{Ah,N}}$ : bilanzierte Ah-Kapazität der Normzyklen

Wenn man davon ausgeht, dass eine Batterie, deren Kapazität im Verlauf der Benutzung auf 80 % des Anfangswertes gesunken ist, nicht mehr die Funktionen erfüllen kann, für die sie bestimmt war, müssen sie bei Erreichen einer Zyklenbelastung von 1 ausgetauscht werden.

Da die Zyklenbelastung als Systemgröße auch nach Austausch einer Batterie weitergezählt wird, wird ein zweiter, batteriebezogener Wert eingeführt, der State of Health, SOH:

$$ SOH = 1 - \Delta \zeta_x $$

  • $\Delta \zeta_x$ : Änderung der Zyklenbelastung seit dem letzten Austausch

Eine Batterie mit $SOH=1$ ist neu, eine Batterie mit $SOH=0$ wird ausgetauscht. Die Lebensdauer ergibt sich im Umkehrschluss aus dem nach der Simulation von einem Jahr erreichten Zyklenbelastung:

$$ t_{\text{ Leben }} = \frac{t_{\text{ Simulation }}}{\zeta} $$

  • $t_{\text{ Leben }}$: Lebensdauer
  • $t_{\text{ Simulation }}$: Simulationszeitraum
  • $\zeta$: Zyklenbelastung

Siehe auch