Nachführung

Je nach Art der Nachführung ändern sich im Simulationsverlauf der Ausrichtungs- und der Neigungswinkel der PV-Module. Für jeden Zeitschritt wird dann aus Neigungs- und Ausrichtungswinkel der PV-Module und dem Sonnenstand der Einfallswinkel der Sonnenstrahlen berechnet.

Nachführungsarten

Nachführungsart	$\alpha_\text{E}$	$\gamma_\text{E}$	Beschreibung
Keine	konstant	konstant	Bei fest montierten Modulen bleiben Neigung und Ausrichtung konstant.
1-achsig Nord-Süd	konstant	variabel	Die PV-Module werden zum Äquator ausgerichtet, während sich die Drehachse in der Nord-Süd-Ebene befindet. Das heißt, sowohl Neigungswinkel als auch Ausrichtungswinkel ändern sich im Verlauf der Simulation.
1-achsig Ost-West	konstant	variabel	Die PV-Module werden so montiert, dass eine Drehung um die Ost-West-Achse ermöglicht wird. Hier ändert sich der Neigungswinkel, nicht jedoch der Ausrichtungswinkel der Module.
1-achsig vertikale Drehachse	variabel	konstant	Die PV-Module werden mit festem Neigungswinkel aufgeständert und über die Drehung der vertikalen Achse dem Sonnenazimut nachgeführt. Das heißt, der Neigungswinkel bleibt konstant, während sich der Ausrichtungswinkel ändert.
2-achsig	variabel	variabel	Hier folgen die PV-Module in Neigung und Ausrichtung der Sonne – beide Winkel ändern sich im Verlauf der Simulation

Einfallswinkel

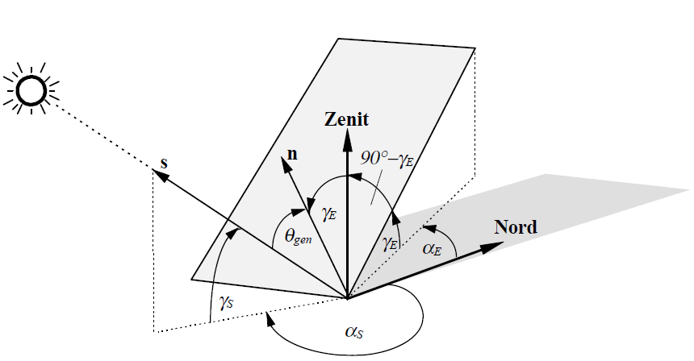
Der Einfallswinkel der Strahlung auf die PV-Module $\theta_\text{gen}$ kann anhand der geometrischen Begebenheiten berechnet werden.

• $\alpha_\text{S}$: Ausrichtung der Sonne
• $\gamma_\text{S}$: Elevation der Sonne
• $\alpha_\text{E}$: Ausrichtung des Moduls
• $\gamma_\text{E}$: Elevation des Moduls

$\cos(\theta_\text{gen}) = - \cos \gamma_S \cdot \sin \gamma_E \cdot \cos (\alpha_S - \alpha_E + \pi) + \sin \gamma_S \cdot \cos \gamma_E$

Quelle der Grafik: Quaschning: “Simulation der Abschattungsverluste bei solarelektrischen Systemen” pdf