Bifaziale Module

Bifaziale Module werden in PV*SOL® wie herkömmliche PV-Module gerechnet, auf die eine erhöhte Einstrahlung trifft. Die erhöhte oder effektive Einstrahlung wird definiert über:

$$ E_\text{effective} = E_\text{front} + E_\text{rear} \cdot BF $$

Der “Bifazialitäts-Faktor” $ BF $ ist eine Datenbank-Angabe des PV-Moduls. Üblich sind Werte zwischen 0.7 und 0.8 (70 bis 80 %). Der Faktor gibt an, wieviel Prozent der auf die Rückseite auftreffenden Leistung vom PV-Modul zur Stromerzeugung genutzt werden können.

Berechnung der Rückseiten-Strahlung

Bei dachparallelen oder fassadenintegrierten Anlagen

Keine Strahlung auf die Rückseite.

Bei vertikalen Modulreihen

Bei Aufständerungswinkeln von mehr als 80° wird die Einstrahlung auf die Vorderseite und die Rückseite mit den gängigen Strahlungsmodellen berechnet.

Bei aufgeständerten Modulreihen

Die Strahlung auf die Modul-Rückseite setzt sich zusammen aus der vom Boden reflektierten Strahlung, der von benachbarten Modulen reflektierten Strahlung und dem Anteil der Diffus- und Direktstrahlung, die direkt die Modul-Rückseite erreichen kann.

$$ E_\text{rear} = E_\text{rear,Boden} + E_\text{rear,Module} +E_\text{rear,diffus} $$

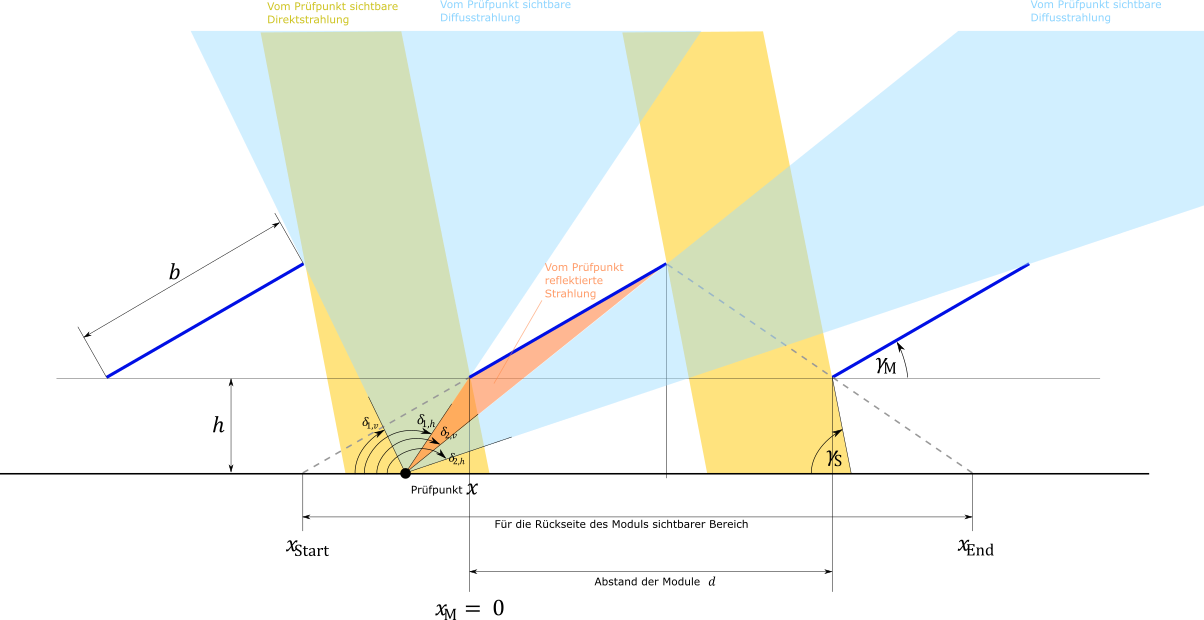
Der für die Rückseite des Moduls sichtbare Bereich des Bodens startet bei $$ x_\text{Start} = x_\text{M} - \frac{h}{\tan⁡ γ_\text{M}} $$ und endet bei $$ x_\text{End} =x_\text{M} +d + \frac{ h(d-b \cos⁡ γ_\text{M})}{(b \sin⁡ γ_\text{M})} $$

mit der Modulbreite b, der Höhe über dem Boden h und dem Modulabstand d.

Es wird für jeden Punkt auf dem für das Modul sichtbaren Bereich des Bodens die eintreffende Strahlung berechnet $$E_\text{In,Prüfpunkt} =E_\text{direkt,Prüfpunkt} +E_\text{diffus,Prüfpunkt} $$

Die direkte Strahlung erreicht den Prüfpunkt in den Bereichen $$ [x_\text{M} + b \cos⁡ γ_\text{M} -d+ \frac{h+b \sin⁡ γ_\text{M}}{\tan⁡ γ_\text{S}} , x_\text{M} + \frac{ h}{\tan⁡ γ_\text{S}} ] $$ und $$ [x_\text{M} + b \cos⁡ γ_\text{M} +\frac{(h+b \sin⁡ γ_\text{M})}{\tan⁡ γ_\text{S}} , x_\text{M} + d + \frac{h}{\tan γ_\text{S}} ] $$

Die diffuse Strahlung erreicht anteilig zum sichtbaren Bereich des Himmels den Prüfpunkt. Vom Prüfpunkt aus sind zwei Bereiche des Himmels sichtbar, zwischen Vorgänger-Modul und Modul, sowie zwischen Modul und Nachfolger-Modul.

Die vordere Begrenzung des vorderen Bereichs verläuft zwischen Prüfpunkt und Oberkante des Vorgänger-Moduls. $$ \tan⁡ δ_\text{(1,v)} = \frac{h+b \sin γ_\text{M}}{b \cos γ_\text{M} -d-x} $$ Die hintere Begrenzung des vorderen Bereichs verläuft zwischen Prüfpunkt und Unterkante des Moduls. $$ \tan⁡ δ_\text{(1,h)} = \frac{h}{x} $$ Die vordere Begrenzung des hinteren Bereichs verläuft zwischen Prüfpunkt und Oberkante des Moduls. $$ \tan⁡ δ_\text{(2,v)} = \frac{h+b \sin⁡ γ_\text{M}}{x+b \cos⁡ γ_\text{M} } $$ Die hintere Begrenzung des hinteren Bereichs verläuft zwischen Prüfpunkt und Unterkante des Nachfolger-Moduls. $$ \tan⁡ δ_\text{(2,h)} = \frac{h}{x+d} $$

Die Diffusstrahlung am Prüfpunkt ergibt sich dann zu

$$ E_\text{diffus,Prüfpunkt} = E_\text{diffus} \frac{(δ_\text{(1,h)}-δ_\text{(1,v)} )+(δ_\text{(2,h)}-δ_\text{(2,v)} )}{180° } $$

Von der Strahlung, die den Prüfpunkt erreicht, wird je nach Albedo ρ ein Teil reflektiert: $$ E_\text{Out,Prüfpunkt} = ρ \cdot E_\text{In,Prüfpunkt} $$

Von dieser als isotrop angenommenen Strahlung erreicht nur ein Teil die Rückseite des Moduls, die noch mit dem Einstrahlungswinkel $ θ_\text{rear,Prüfpunkt} $ gewichtet wird: $$ E_\text{Out,Prüfpunkt,Modul} = E_\text{Out,Prüfpunkt} \frac{ δ_\text{(1,h)}-δ_\text{(2,v)}}{180° } \cdot IAM \cdot θ_\text{rear,Prüfpunkt} \cdot (1-f_\text{Shading by structure} ) $$

Der mittlere Einstrahlwinkel wird angenähert durch

$$ θ_\text{rear,Prüfpunkt} = \frac{δ_\text{(1,h)}+δ_\text{(2,v)}}{2} - γ_\text{M} $$

Die Berechnung wird für $ n $ Prüfpunkte zwischen $ x_\text{Start} $ und $ x_\text{End} $ wiederholt, wobei jede Einstrahlung auf den Prüfpunkt mit $ (x_\text{End} - x_\text{Start} )/n $ gewichtet wird. Anschließend wird über alle $ E_\text{Out,Prüfpunkt,Modul} $ integriert und man erhält die vom Boden reflektierte Strahlung auf die Modul-Rückseite.

$$ E_\text{rear,Boden} = \sum_{i=0}^{n} E_\text{Out,Prüfpunkt,Modul, i} (x_\text{End} - x_\text{Start} )/n $$

$ E_\text{rear,diffus} $ entspricht dem Anteil der Diffusstrahlung, die von der Rückseite des Moduls aus sichtbar ist.

$$ E_\text{rear,diffus} =E_\text{diffus} \frac{γ_\text{M} -γ_\text{M,next} }{180°} $$

Der Winkel von der Unterkante des Moduls zur Oberkante des nächsten Moduls $ γ_\text{M,next} $ berechnet sich mit $$ \tan⁡γ_\text{M,next} = \frac{b \sin⁡ γ_\text{M}}{d+b \cos⁡ γ_\text{M} } $$

Siehe auch

• Navigationsseiten > PV-Module > Bifaziale Module