Kennlinienmodelle
Um die Kennlinie einer Solarzelle zu beschreiben, bedient man sich eines Modells, dessen Aufgabe es ist, das elektrische oder auch thermische Verhalten der Zelle über einen möglichst breiten Bereich äußerer Einflüsse darzustellen.
Grundsätzlich können die Modelle in empirische und physikalisch orientierte unterschieden werden. Empirische Modelle basieren auf Messergebnissen von realen Photovoltaikmodulen oder -zellen, aus denen gewöhnlich Parameter für Fitfunktionen gewonnen werden. Diese Modelle können für die vermessenen Module eine sehr hohe Abbildungsgenauigkeit erreichen, während sie erwartungsgemäß schlechter bei nicht vermessenen Modulen funktionieren, da hier keine Parameter bestimmt wurden.
Physikalische Modelle versuchen, die realen Vorgänge im photovoltaischen Halbleiter allgemeingültig darzustellen. Dadurch können sie auch auf nur minimal (vom Hersteller) vermessene Module mit einiger Genauigkeit angewendet werden. Jedoch setzen auch die physikalischen Modelle einige Parameter voraus, die entweder ebenfalls empirisch ermittelt werden müssen oder in Form von Standardwerten in die Modellierung einfließen. Die am weitesten verbreiteten physikalischen Modelle sind das Ein- und Zwei-Dioden-Modell.
In PV*SOL® wird zur Berechnung der Kennlinien entweder das PV*SOL® Modell oder das Zwei-Dioden-Modell verwendet.
PV*SOL® Modell
Grundlagen
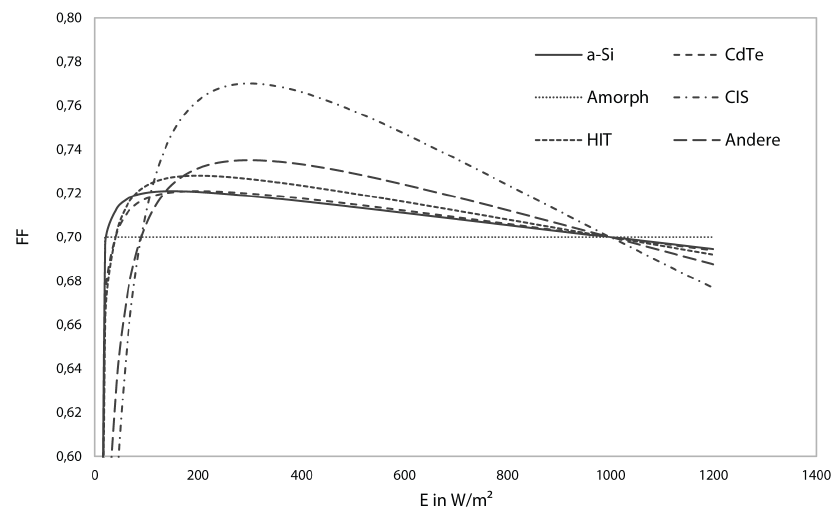
Es ist in erster Linie ein mathematisches Modell, das jedoch neben den vom Hersteller gelieferten elektrischen Daten als unbedingte Eingangsgrößen einen weiteren Satz elektrischer Daten bei einem Schwachlicht-Punkt in der Nähe von $20,%$ der STC-Einstrahlung benötigt. Es macht sich dabei den charakteristischen Verlauf des Füllfaktors in Abhängigkeit von der Einstrahlung zu Nutze. Da der Kurzschluss-Strom weitgehend linear von der Einstrahlung ist, können mit der Füllfaktor-Funktion daraus die Größen im MPP abgeleitet werden. Sind diese Größen berechnet, wird zwischen den drei Punkten exponentiell interpoliert. So ermöglicht das Modell von PV*SOL® die direkte Berechnung sowohl der Schlüsselparameter als auch der Kennlinie eines Moduls bei gegebener Einstrahlung.
Der Schwachlicht-Punkt
Sind die zusätzlich notwendigen Informationen über den Schwachlicht-Punkt nicht gegeben – im Idealfall werden diese von den Modulherstellern zur Verfügung gestellt – werden in Abhängigkeit von der Modultechnologie Standardwerte berechnet.
Hierzu werden zunächst einige Parameter bestimmt. Die Einstrahlung im Schwachlicht-Punkt $E_\text{SL}$ legt fest, wo der Füllfaktor den (maximalen) Wert $ff_\text{Extra} \cdot FF_\text{STC}$ annimmt. Die Parameter $E_\text{min}$ und $k$ dienen der iterativen Bestimmung der übrigen Kenngrößen.
Es wird also zunächst der Füllfaktor im Schwachlicht-Punkt $FF_\text{SL}$ berechnet:
$$ FF_\text{SL} = ff_\text{Extra} \cdot FF_\text{STC} \qquad\qquad (1)$$
Die Leerlaufspannung im Schwachlicht-Punkt $U_\text{OC,SL}$ wird bestimmt über
$$ U_\text{OC,SL} = U_\text{OC,STC} \cdot \frac{\log{ \left( \frac{E_\text{SL}}{E_\text{min}}\right)}}{\log{ \left( \frac{E_\text{STC}}{E_\text{min}}\right)}} \qquad\qquad (2)$$
Tabelle 2: Standardwerte des PV*SOL® -Modells für verschiedene Modul-Technologien
| Modultechnologie | $E_\text{SL}$ | $E_\text{min}$ | $k$ | $ff_\text{Extra}$ |
|---|---|---|---|---|
| Amorphes Si | $150$ | $2.2\cdot 10^{-6}$ | $0.9685$ | $1.03$ |
| CdTe | $200$ | $1.0\cdot 10^{-7}$ | $1.0000$ | $1.03$ |
| Amorph | $250$ | $5.0\cdot 10^{-8}$ | $1.0300$ | $1.00$ |
| CIS | $300$ | $0.1$ | $1,0000$ | $1.10$ |
| HIT | $200$ | $1.0\cdot 10^{-7}$ | $1.0400$ | $1.04$ |
| Alle anderen | $300$ | $0.1$ | $1.0000$ | $1.05$ |
Je kleiner also $E_\text{min}$ und je größer $E_\text{SL}$ gewählt werden, desto geringer fällt die Abnahme der Leerlauf-Spannung im Schwachlicht-Punkt aus (siehe Beispiel in Abbildung 4 mit $U_\text{OC,STC}=0.6,\text{V}$).
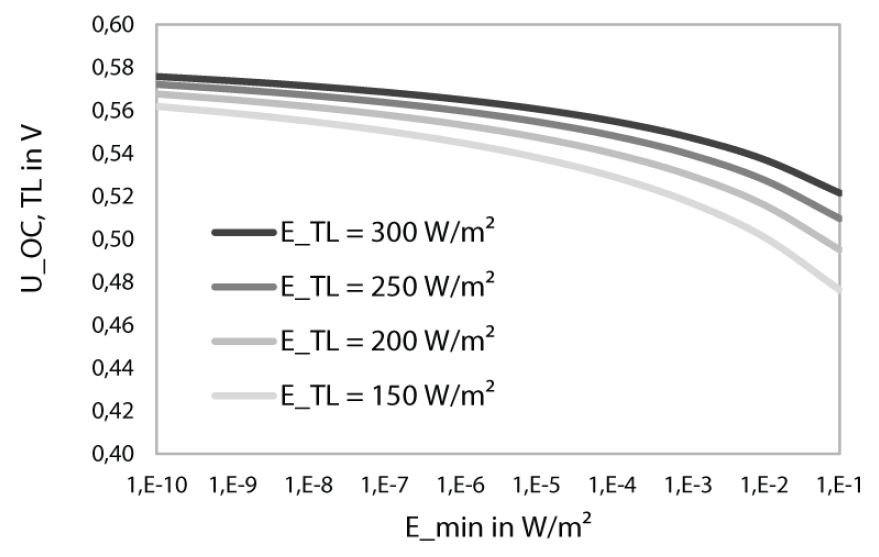
Abbildung 4: Die Schwachlicht-Leerlaufspannung in Abhängigkeit von $E\_\text{min}$ und $E\_\text{SL}$.
Der Kurzschlussstrom wird wie eingangs erwähnt linear heruntergerechnet gemäß
$$ I_\text{SC,TL} = I_\text{SC,STC} \frac{E_\text{TL}}{E_\text{STC}} \qquad\qquad (3)$$
Der Strom und die Spannung im MPP werden zunächst gleich $U_\text{MPP,SL} = 1,1\cdot U_\text{OC,SL}$ und $I_\text{MPP,SL}=0$ gesetzt. Im Anschluss werden die Gleichungen für den Strom
$$ I_\text{MPP,SL}=k\cdot I_\text{SC,SL} \frac{I_\text{MPP,STC}}{I_\text{SC,STC}} \qquad\qquad (4)$$
und die Spannung
$$ U_\text{MPP,SL} = FF_\text{SL} \cdot U_\text{OC,SL} \frac{I_\text{SC,STC}}{I_\text{MPP,STC}} \qquad\qquad (5)$$
im MPP, sowie die Korrektur des Faktors $k$ mit
$$ k = 1,1 \frac{U_\text{MPP,SL}}{U_\text{OC,SL}} \qquad\qquad (6)$$
solange wiederholt, bis $U_\text{MPP,SL}\gt U_\text{OC,SL}$ oder $k\gt 2$. Sind die Schwachlicht-Größen bestimmt, können sie im Folgenden für jede Einstrahlung und Temperatur berechnet werden.
Füllfaktor
Das charakteristische Verhalten des Füllfaktors $FF$ wird nun über die Inverse einer quadratischen Gleichung abgebildet, wobei $E$ der Globalstrahlung auf Modul-Ebene entspricht:
$$ FF=\frac{E}{a\cdot E^{2} + b\cdot E + c} \qquad\qquad (7)$$
Die Koeffizienten $a$, $b$ und $c$ werden je nach Größe des Schwachlicht-Füllfaktors wie folgt berechnet:
$$ a = \begin{cases} 0 &\text{wenn } FF_\text{SL} = FF_\text{STC}\cr \frac{E_\text{ STC} \left( FF_\text{ SL}-FF_\text{ STC} \right) }{FF_\text{ SL}\cdot FF_\text{ STC}\cdot \left( E_\text{ SL}-E_\text{ STC} \right) ^2} &\text{wenn } FF_\text{ SL}\gt FF_\text{ STC}\cr \frac{E_\text{ SL} \left( FF_\text{ STC}-FF_\text{ SL} \right)}{FF_\text{ STC}\cdot FF_\text{ SL}\cdot \left( E_\text{ STC}-E_\text{ SL} \right) ^2} &\text{wenn } FF_\text{ SL}\lt FF_\text{ STC}\cr \end{cases} \qquad\qquad (8) $$
$$ b = \begin{cases} \frac{1}{FF_\text{SL}} &\text{wenn } FF_\text{SL} = FF_\text{STC}\cr \frac{1-2a \cdot E_\text{SL}FF_\text{SL}}{FF_\text{SL}} &\text{wenn } FF_\text{SL} \neq FF_\text{STC}\cr \end{cases} \qquad\qquad (9) $$
$$ c = \begin{cases} 0 &\text{wenn } FF_\text{SL} = FF_\text{STC}\cr a \cdot E_\text{SL}^{2} &\text{wenn } FF_\text{SL} \gt FF_\text{STC}\cr a \cdot E_\text{STC}^{2} &\text{wenn } FF_\text{SL} \lt FF_\text{STC}\cr \end{cases} \qquad\qquad (10) $$
Zur Veranschaulichung sind in Abbildung 5 die verschiedenen Verläufe für den Füllfaktor in Abhängigkeit der Einstrahlung dargestellt. Als fiktiver Füllfaktor bei STC-Bedingungen wurde für alle Technologien 0,7 angenommen.
Leerlauf
Analog zur Berechnung im Schwachlicht-Punkt nach Gleichung (2-1-2) wird die Leerlaufspannung $ U_\text{OC} $ nun mit
$$ U_\text{OC} = U_\text{OC,STC} \cdot \frac{\ln\left(\frac{E}{G_0}\right)}{\ln\left(\frac{E_\text{STC}}{G_0}\right)} + \alpha_\text{U} \left(T_\text{M}-T_\text{STC}\right) \qquad\qquad (11)$$
berechnet, wobei beachtet werden muss, dass der Temperaturkoeffizient der Spannung $\alpha_\text{U}$ hier in $\frac{\text{V}}{\text{K}}$ eingesetzt werden muss. Die Hilfsgröße $G_0$ sorgt dafür, dass die Leerlaufspannung bei Teillast gleich $U_\text{OC,SL}$ ist:
$$ G_0 = \exp\left( \frac{U_\text{OC,STC}\ln(E_\text{SL}) - U_\text{OC,SL}\ln(E_\text{STC})}{U_\text{OC,STC} - U_\text{OC,SL}} \right)\qquad\qquad (12)$$
Kurzschlussstrom
Die Berechnung des Kurzschluss-Stromes $I_\text{SC}$ erfolgt nun abhängig davon, ob die aktuelle Einstrahlung $E$ kleiner oder größer ist als die Einstrahlung im Schwachlicht-Punkt $E_\text{SL}$. Ist sie geringer, gilt der quadratische Zusammenhang
$$ I_\text{SC} = d \cdot E^2 + \left( e + \frac{\Delta I_\text{SC}}{E_\text{STC}} \right) E \qquad\qquad (13)$$
mit
$$ d = \frac{I_\text{SC,STC} - \left( \frac{I_\text{SC,STC}-I_\text{SC,SL}}{E_\text{STC}-E_\text{SL}} \right) E_\text{STC}}{E_\text{SL}^2} \qquad\qquad (14)$$
und
$$ e = \frac{I_\text{SC,STC} - I_\text{SC,SL}}{E_\text{STC}-E_\text{SL}} + 2 \frac{I_\text{SC,STC} - \left( \frac{I_\text{SC,STC}-I_\text{SC,SL}}{E_\text{STC}-E_\text{SL}} \right) E_\text{STC}}{E_\text{SL}} \qquad\qquad (15)$$
Die Temperaturabhängigkeit fließt über
$$ \Delta I_\text{SC} = \alpha_\text{I,SC} \left( T_\text{M} - T_\text{STC} \right) \qquad\qquad (16)$$
mit in die Berechnung ein (auch hier muss der absolute Wert benutzt werden, also $[\alpha_\text{I}] = \frac{\text{A}}{\text{K}}$). Ist die Einstrahlung größer als die des Schwachlicht-Punktes, ergibt sich ein linearer Zusammenhang zwischen Kurzschluss-Strom und Einstrahlung, wie er allen Modellen gleich ist:
$$ I_\text{SC} = I_\text{SC,STC} - \left( \frac{I_\text{SC,STC} - I_\text{SC,SL}}{E_\text{STC} - E_\text{SL}} \right) E_\text{STC} + \left( \frac{I_\text{SC,STC} - I_\text{SC,SL}}{E_\text{STC} - E_\text{SL}} + \frac{\Delta I_\text{SC}}{E_\text{STC}} \right) E \qquad\qquad (17)$$
MPP
Auch die Berechnung des MPP-Stromes wird in zwei Bereiche unterteilt – entsprechend der Berechnung des Kurzschluss-Stromes. Im Bereich der Einstrahlung zwischen $0$ und dem Schwachlicht-Punkt gilt die Vorschrift
$$ I_\text{MPP} = I_\text{SC} \cdot \upsilon_\text{I} \cdot \sqrt{\zeta_\text{P}} \qquad\qquad (18)$$
mit
$$ \upsilon_\text{I} = b\upsilon_\text{I} + m\upsilon_\text{I} \cdot E \cdot \sqrt{\zeta_\text{P}} \qquad\qquad (19)$$
$$ b\upsilon_\text{I} = \frac{I_\text{MPP,STC}}{I_\text{SC,STC}} - \left( \frac{ \frac{I_\text{MPP,STC}}{I_\text{SC,STC}} - \frac{I_\text{MPP,SL}}{I_\text{SC,SL}} }{E_\text{STC} - E_\text{SL}} \cdot E_\text{STC} \right) \qquad\qquad (20)$$
$$ m\upsilon_\text{I} = \frac{ \frac{ I_\text{MPP,STC}}{I_\text{SC,STC}} - \frac{I_\text{MPP,SL}}{I_\text{SC,SL} }}{ E_\text{STC} - E_\text{SL} }\qquad\qquad (21)$$
und dem von Temperaturkoeffizienten der Leistung $\alpha_\text{P}$ (diesmal als Wert zwischen $0$ und $1$) abhängigen
$$ \zeta_\text{P} = \frac{ ( 1+\alpha_\text{P} (T_\text{M}-T_\text{STC} ))(U_\text{OC,STC} I_\text{SC,STC}) }{ (U_\text{OC,STC} + \Delta U_\text{OC}) (I_\text{SC,STC} + \Delta I_\text{SC}) } \qquad\qquad (22)$$
Analog zum Strom wird $\Delta U_\text{OC}$ berechnet:
$$ \Delta U_\text{OC} = \alpha_\text{U} (T_\text{M}-T_\text{STC}) \qquad\qquad (23)$$
Liegt die Einstrahlung oberhalb des Schwachlicht-Punktes, wird der MPP-Strom einfach mit dem Verhältnis aus MPP- und Kurzschlussstrom bei STC-Bedingungen skaliert und man erhält
$$ I_\text{MPP} = \frac{I_\text{MPP,STC}}{I_\text{SC,STC}} \cdot I_\text{SC} \qquad\qquad (24)$$
Damit sind die drei Kennpunkte Kurzschluss, Leerlauf und MPP berechnet.
Kennlinie
Zwischen diesen Punkten kann die Kennlinie exponentiell interpoliert werden. Im Bereich zwischen Kurzschluss und MPP gilt dabei
$$ I_1(U) = bv + mv \cdot \exp(U\cdot kv) - \frac{I_\text{SC} - I_\text{MPP}}{2 U_\text{MPP}} \cdot U \qquad\qquad (25)$$
mit
$$ bv = \frac{ I_\text{SC}\cdot\exp(kv\cdot U_\text{MPP}) - \left( I_\text{MPP} + \frac{I_\text{SC} - I_\text{MPP}}{2} \right) }{ \exp(kv\cdot U_\text{MPP})-1 } \qquad\qquad (26)$$
$$ mv = \frac{ I_\text{MPP}-I_\text{SC}+\frac{I_\text{SC}-I_\text{MPP}}{2} }{ \exp(kv\cdot U_\text{MPP})-1 } \qquad\qquad (27)$$
$$ kv = \frac{\text{invers}(y)}{U_\text{MPP}} \qquad\qquad (28)$$
$$ y = \left( \frac{I_\text{MPP} + \frac{I_\text{SC}-I_\text{MPP}}{2} }{ I_\text{SC} - I_\text{MPP} + \frac{I_\text{SC}-I_\text{MPP}}{2} } \right) \qquad\qquad (29)$$
Die Funktion $\text{invers}(y)$ liefert eine Annäherung des $x$-Wertes für ein bekanntes $y$ der Funktion
$$ y = \frac{x}{\exp(x-1)} \qquad\qquad (30)$$
da dies nicht explizit berechenbar ist.
Im zweiten Bereich – zwischen MPP und Leerlauf – wird die Kennlinie folgendermaßen angenähert:
$$ I_2(U) = bn + mn \exp(U\cdot kn) - \frac{I_\text{SC} - I_\text{MPP}}{2U_\text{MPP}} (U-U_\text{OC}) \qquad\qquad (31)$$
mit
$$ bn = \frac{I_\text{MPP}-I_\text{rd}}{1-\exp(kn(U_\text{MPP}-U_\text{OC}))} \qquad\qquad (32)$$
$$ mn = \frac{ -I_\text{MPP}+I_\text{rd} }{ \exp(kn\cdot U_\text{OC}) - \exp(kn\cdot U_\text{MPP}) } \qquad\qquad (33)$$
$$ kn = \frac{ \text{invers}(y) }{U_\text{OC} - U_\text{MPP}} \qquad\qquad (34)$$
$$ y = \frac{ U_\text{OC} }{U_\text{MPP}} - 1 \qquad\qquad (35)$$
$$ I_\text{rd} = \frac{ I_\text{SC}-I_\text{MPP} }{ 2\cdot U_\text{MPP} } (U_\text{OC} - U_\text{MPP}) \qquad\qquad (36)$$
Ein-Dioden-Modell
Grundlagen
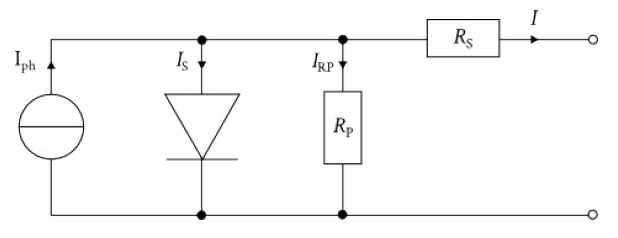
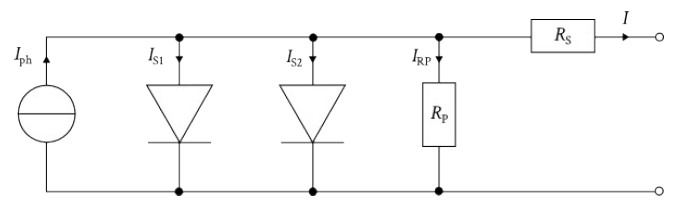
Erweitert man das Ersatz-Schaltbild einer PV-Zelle, das aus einer Stromquelle mit parallel geschalteter Diode besteht, um einen Parallel- ($R_\text{P}$) und einen Serienwiderstand ($R_\text{S}$), erhält man das Schaltbild des Ein-Dioden-Modells:
Die Stromquelle modelliert im Prinzip die Generation von Elektron-Loch-Paaren, die durch die Spannung im p-n-Übergang getrennt und dann über eine externe Last abgeleitet werden. Der p-n-Übergang selbst wird im Schaltbild durch die Diode repräsentiert. Rekombinationen der Elektron- Loch-Paare, wie sie zum Beispiel am Rand der Zelle auftreten, wird durch den Parallelwiderstand Rechnung getragen, während der Serienwiderstand die Verluste durch Kontakte, Leitungen und dergleichen widerspiegelt.
Demnach kann der Strom, der der Zelle bei einer bestimmten Spannung an den Klemmen entnommen werden kann, wie folgt als Erweiterung der Shockley-Gleichung formuliert werden:
$$ I = I_\text{ph} - I_\text{S} \cdot \left( \exp\left( \frac{U+IR_\text{s}}{m\cdot U_\text{T}} \right)-1 \right) - \frac{U+IR_\text{s}}{R_\text{p}} \qquad\qquad (37)$$
Der Photostrom $I_\text{ph}$ liegt demnach immer etwas über dem aktuell zu messenden Strom, bei STC-Bedingungen also etwas über dem Kurzschlussstrom $I_\text{SC,STC}$. Er ist linear abhängig von der Einstrahlung $E$ und steigt mit zunehmender Zelltemperatur $T$:
$$ I_\text{ph} = (C_1+C_2\cdot T)E \qquad\qquad (38)$$
Die Parameter $C_1$ und $C_2$ sind zell- bzw. modulabhängig, lassen sich aber einfach aus den Herstellerangaben zumindest näherungsweise berechnen.
Der Sättigungsstrom $I_\text{S}$ kann mit
$$ I_\text{S} = C_\text{S} T^{\kappa} \exp\left( -\frac{E_\text{Gap}}{m\text{k}T} \right) \qquad\qquad (39)$$
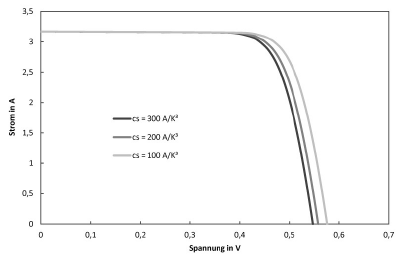
näher beschrieben werden und liegt üblicherweise in eienr Größenordnung von $10^{-11}…10^{-9}\text{A}$. Die material- und technologieabhängige Konstante $C_\text{S}$ weist Werte um die $10^{2}\frac{\text{A}}{\text{K}^3}$ auf, der Exponent der Temperatur $\kappa$ wird in der Literatur meist mit $3$ angegeben, $E_\text{Gap}$ ist der Bandabstand des Zellmaterials (z.B. $E_\text{Gap,Si}(T=300\text{K})\approx 1,12\text{eV}$ von Silizium bei Raumtemperatur). Die Temperatur- oder Thermospannung $U_\text{T}$ wird mit
$$ U_\text{T} = \frac{\text{k}T}{e} \qquad\qquad (40)$$
berechnet; manchmal wird der Diodenfaktor $m$ noch in die Berechnung einbezogen. Letztendlich ist es aber natürlich gleichwertig, den Diodenfaktor separat und nicht als Teil der Thermospannung aufzufassen. Physikalisch soll der Diodenfaktor Rekombinationseffekte u. A. im p-n Übergang darstellen. In der Literatur wird in den meisten Fällen $m=1$ gesetzt, wobei zu bezweifeln ist, dass alle Zelltechnologien ein ähnelndes Rekombinationsverhalten aufweisen.
Schließlich bleiben zur Beschreibung der in Gleichung $(37)$ verwendeten Formelzeichen noch der Serienwiderstand $R_\text{s}$ und der Parallelwiderstand $R_\text{p}$. Bei modernen Solarzellen sollten die Widerstände im Bereich $R_\text{s}=10^{-1}\Omega$ bzw. $R_\text{p}=10^2\Omega$ liegen.
Der Serienwiderstand kann als weitgehend unabhängig von Einstrahlung und Temperatur angenommen werden, während der Parallelwiderstand der Einstrahlung $E$ umgekehrt proportional ist.
$$ R_\text{p}(E) = R_\text{p,STC}\frac{E_\text{STC}}{E} \qquad\qquad (41)$$
Randbedingungen
Im Allgemeinen lassen sich unter STC-Bedingungen aus der Kennlinien-Gleichung $(37)$ die vier Situationen, die durch die Datenblattangaben definiert sind, wie folgt beschreiben. Im Leerlauf nimmt die Spannung den Wert der auf dem Datenblatt angegebenen Leerlaufspannung $U_\text{OC,STC}$ an, der Strom wird $0$:
$$ 0 = I_\text{ph}-I_\text{S}\cdot\left( \exp\left( \frac{U_\text{OC,STC}}{mU\text{T}} \right)-1 \right) - \frac{U_\text{OC,STC}}{R_\text{p}} \qquad\qquad (42)$$
Im Kurzschluss wird wiederum die Spannung $0$, während der Strom den Datenblattwert annimmt:
$$ I_\text{SC,STC} = I_\text{ph}-I_\text{S} \cdot \left( \exp\left( \frac{I_\text{SC,STC} \cdot R_\text{s}}{m \cdot U_\text{T}} \right)-1 \right)-\frac{I_\text{SC,STC} \cdot R_\text{s}}{R_\text{p}} \qquad\qquad (43)$$
Im Punkt maximaler Leistung (MPP) sind die Ströme und Spannung ebenfalls gegeben:
$$ I_\text{MPP,STC} = I_\text{ph}-I_\text{S}\left( \exp\left( \frac{U_\text{MPP,STC}+I_\text{MPP,STC}\cdot R_\text{s}}{m\cdot U_\text{T}} \right)-1 \right)-\frac{U_\text{MPP,STC}+I_\text{SC,STC}\cdot R_\text{s}}{R_\text{p}} \qquad\qquad (44)$$
Des Weiteren muss die Steigung der Leistung im MPP gleich $0$ sein. Also gilt:
$$ \frac{dP}{dU}(U=U_\text{MPP,STC})\stackrel{!}{=}0 $$
$$ I_\text{ph}-C_\text{S}T^3\exp\left( -\frac{E_\text{Gap}}{m\text{k}T} \right) \cdot \left( \exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC} \cdot R_\text{S}}{m\cdot U_\text{T}} \right) -1 \right)-\frac{U_\text{MPP,STC}+I_\text{SC,STC}\cdot R_\text{S}}{R_\text{P}} $$ $$+ U_\text{MPP,STC}\cdot\left(-\frac{C_\text{S}T^{2}}{m\cdot U_\text{T}}\cdot\exp\left(-\frac{E_\text{Gap}}{mkT}\right)\cdot\left(\frac{U_\text{MPP,STC} + I_\text{MPP,STC} \cdot R_\text{S}}{m\cdot U_\text{T}}\right)-\frac{1}{R_\text{P}}\right)\stackrel{!}{=} 0 \qquad (45) $$
Dynamik
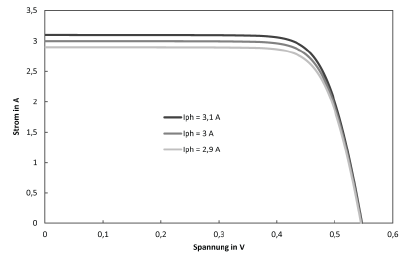
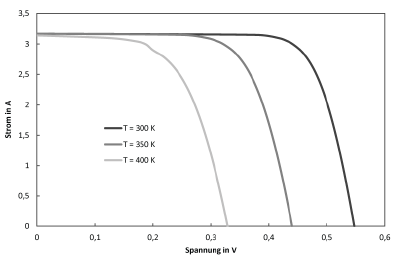
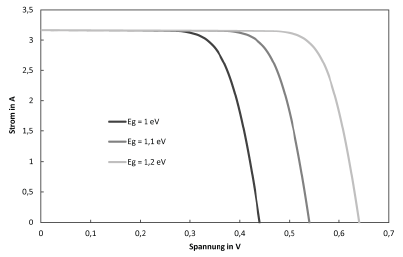
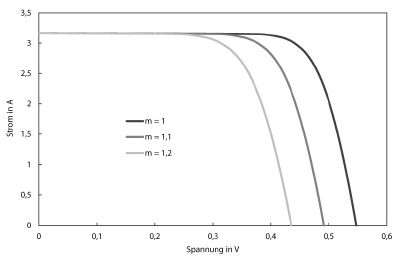
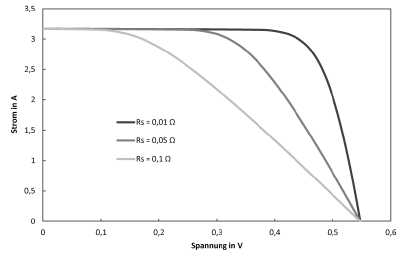
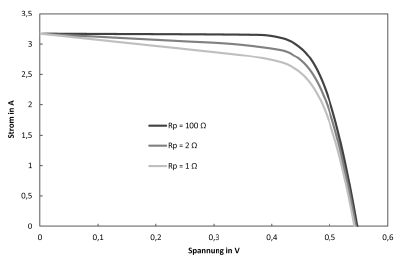
Um einschätzen zu können, wie das Ein-Dioden-Modell auf die verschiedenen Parameter reagiert, werden im Folgenden I-U-Kennlinien dargestellt, bei denen jeweils ein Parameter variiert wird. Soweit nicht anders im Diagramm angegeben, wurden die Parameter so definiert:
$$I_\text{ph}=3,17,\text{A} \qquad T=300,\text{K} \qquad E_\text{Gap}=1,107,\text{eV}$$ $$m=1 \qquad R_\text{s}=0,01,\Omega \qquad R_\text{p}=100,\Omega \qquad C_\text{S}=300,\frac{\text{A}}{\text{K}^3}$$
Parameterbestimmung
Im Normalfall sind den Datenblättern der PV-Modulhersteller lediglich die elektrischen Eckdaten bei STC-Bedingungen des Module zu entnehmen. Hierzu gehören die Leerlaufspannung $U_\text{OC,STC}$, der Kurzschlussstrom $I_\text{SC,STC}$, Spannung und Strom im MPP $U_\text{MPP,STC}$ und $I_\text{MPP,STC}$, sowie in den meisten Fällen die Temperaturkoeffizienten der Leerlaufspannung $\alpha_\text{U}$ und des Kurzschlussstroms $\alpha_\text{I}$.
Aus diesen Angaben können die Parameter des Ein-Dioden-Modells berechnet werden.
Zwei-Dioden-Modell
Grundlagen
Das Zwei-Dioden-Modell fügt dem oben beschriebenen Ein-Dioden-Modell eine weitere Diode parallel zur ersten hinzu, was im Allgemeinen zu einer Verbesserung der Abbildungsgenauigkeit im Bereich des MPP beiträgt.
Dem rechnerischen Modell für die Kennlinie wird dementsprechend ein weiterer Term hinzugefügt. Die Diodenfaktoren $m_1$ und $m_2$ werden in der Regel gleich 1 bzw. 2 gesetzt, und auch die Sättigungsströme $I_\text{S1}$ und $I_\text{S2}$ unterscheiden sich im Betrag.
$$ I=I_\text{ph} - I_\text{S1} \cdot \exp\left(\frac{U + I\cdot R_\text{S}}{m_1\cdot U_\text{T}}\right) - I_\text{S2}\cdot\exp\left( \frac{U + I\cdot R_\text{S}}{m_2\cdot U_\text{T}} \right) - \frac{U + I\cdot R_\text{S}}{R_\text{P}} \qquad\qquad (46)$$
Der Photostrom $I_\text{ph}$ wird analog zum Ein-Dioden-Modell nach Gleichung (38) berechnet. Die Sättigungsströme werden über
$$ I_\text{S1}=C_\text{S1}\cdot T^{\kappa_1} \cdot \exp\left( -\frac{E_\text{Gap}}{m_1\cdot k \cdot T} \right) \qquad\qquad (47)$$
und
$$ I_\text{S2}=C_\text{S2}\cdot T^{\kappa_2} \cdot \exp\left( -\frac{E_\text{Gap}}{m_2\cdot k \cdot T} \right) \qquad\qquad (48)$$
berechnet. Die Exponenten $\kappa_1$ und $\kappa_2$ werden in der Literatur nahezu einstimmig mit $3$ und $\frac{5}{2}$ angegeben. Damit enthält das Zwei-Dioden-Modell zwei Parameter mehr als das Ein-Dioden-Modell: Den Diodenfaktor $m_2$ und den Sättigungsfaktor $C_\text{S2}$. Darüber hinaus gibt es Ansätze, die den genauen Wert der Exponenten der Temperaturen $\kappa_1$ und $\kappa_2$ in den Gleichungen für die Sättigungsströme hinterfragen und zu von $3$ und $\frac{5}{2}$ abweichenden Werten gelangen.
Randbedingungen
Analog zum Ein-Dioden-Modell können die vier Randbedingungen aufgestellt werden. Die Leerlauf-Gleichung
$$ 0=I_\text{ph}-I_\text{S1}\cdot \left( \exp\left( \frac{U_\text{OC,STC}}{m_1 \cdot U_\text{T}} \right)-1 \right) - I_\text{S2}\cdot\left(\exp\left( \frac{U_\text{OC,STC}}{m_2\cdot U_\text{T}} \right)-1 \right)-\frac{U_\text{OC,STC}}{R_\text{P}} \qquad\qquad (49)$$
die Kurzschluss-Gleichung
$$ I_\text{SC,STC}=I_\text{ph}-I_\text{S1}\cdot \exp\left( \frac{I_\text{SC,STC}\cdot R_\text{S}}{m_1\cdot U_\text{T}} \right)-I_\text{S2}\cdot \exp\left( \frac{I_\text{SC,STC}\cdot R_\text{S}}{m_2\cdot U_\text{T}} \right)-\frac{I_\text{SC,STC}\cdot R_\text{S}}{R_\text{P}} \qquad\qquad (50)$$
und die beiden Gleichungen für den MPP
$$ I_\text{MPP,STC} = I_\text{ph} - I_\text{S1}\cdot \exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC}\cdot R_\text{S}}{m_1\cdot U_\text{T}} \right) $$ $$ -I_\text{S2}\cdot\exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC}\cdot R_\text{S}}{m_2\cdot U_\text{T}} \right) - \frac{U_\text{MPP,STC} + I_\text{MPP,STC}\cdot R_\text{S}}{R_\text{P}} \qquad\qquad (51)$$
und
$$ \frac{dP}{dU}\left(U=U_\text{MPP,STC}\right)\stackrel{!}{=}0 $$
$$ I_\text{ph}-I_\text{S1}\cdot \exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC} \cdot R_\text{S}}{m_1\cdot U_\text{T}} \right) - I_\text{S2}\cdot \exp\left(\frac{U_\text{MPP,STC} + I_\text{MPP,STC} \cdot R_\text{S}}{m_2\cdot U_\text{T}} \right) $$ $$ - \frac{U_\text{MPP,STC} + I_\text{MPP,STC} \cdot R_\text{S}}{R_\text{P}} $$ $$ +U_\text{MPP,STC}\cdot\left( -\frac{e\cdot C_\text{S1}T^2}{m_1\cdot k}\cdot\exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC}\cdot R_\text{S}}{m_1\cdot U_\text{T}} \right) - \frac{e\cdot C_\text{S2}\cdot T^{\frac{3}{2}}}{m_2\cdot k} \exp\left( \frac{U_\text{MPP,STC} + I_\text{MPP,STC}\cdot R_\text{S}}{m_2\cdot U_\text{T}}\right)-\frac{1}{R_\text{P}}\right)\stackrel{!}{=}0 \qquad (52)$$
Dynamik
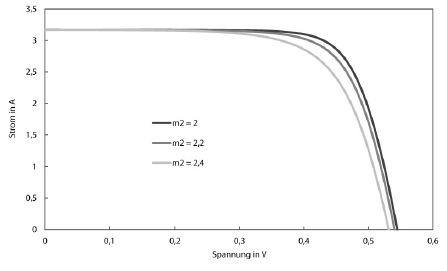
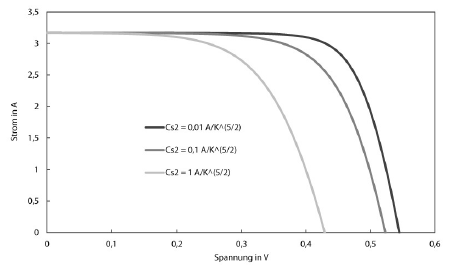
Im Wesentlichen verhält sich die I-U-Kennlinie des Zwei-Dioden-Modells bei der Variation der Parameter ähnlich wie beim Ein-Dioden-Modell. Der Vollständigkeit wegen seien hier die Variationen der beiden neuen Parameter dargestellt:
Zu erkennen ist, dass die Kennlinie weniger sensibel auf die Variation des zweiten Diodenfaktors reagiert als auf die des ersten. Grund hierfür ist einerseits, dass der zweite Diodenfaktor um Größenordnungen kleiner ist als der erste ($C_\text{S2} \approx 10^{-2} ~\text{A} \cdot \text{K}^{-\frac{5}{2}}$), andererseits wird die Temperatur in diesem Term geringer potenziert.
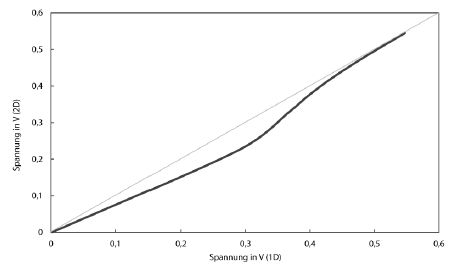
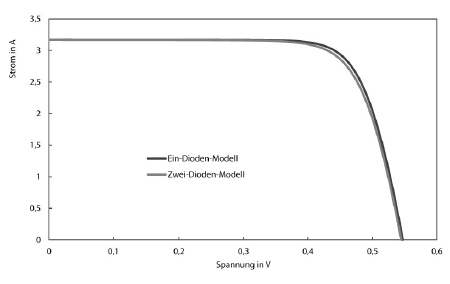
Wie genau sich der zweite Term auf die Kennlinie auswirkt, soll Abbildung 17 verdeutlichen. Die mit dem Zwei-Dioden- wurde über der mit dem Ein-Dioden-Modell berechneten Spannung aufgetragen. Zu beachten ist, dass sich der zweite Diodenterm am prägnantesten im Bereich unterhalb der MPP-Spannung auswirkt. Im Kurzschluss- und Leerlaufpunkt liefert das Zwei-Dioden-Modell jedoch keine abweichenden Ergebnisse. In Abbildung 18 sind die I-U-Kennlinien beider Modelle zusammen aufgetragen.
Parameterbestimmung
Im Zwei-Dioden-Modell kommen durch den zweiten Diodenterm zu den bereits im Ein-Dioden-Modell zu bestimmenden Parametern noch zwei weitere hinzu.
- Der zweite Sättigungsfaktor $C_\text{S2}$ und
- der zweite Diodenfaktor $m_2$
Man erhält also ein System mit zunächst acht Unbekannten. Da sich auch in diesem Fall der Bandabstand $E_\text{Gap}$ und die Diodenfaktoren $m_1$ und $m_2$ nicht explizit berechnen lassen, werden sie durch die in der Literatur üblichen Werte ersetzt.
Unter diesen Voraussetzungen ist es möglich, die Parameter für das Zwei-Dioden-Modell aus Datenblattangaben zu berechnen.
Siehe auch