Bifacial modules

Bifacial modules are calculated in PV*SOL® like conventional PV modules, which are subject to increased irradiation. The increased or effective irradiation is defined via:

$$ E_\text{effective} = E_\text{front} + E_\text{rear} \cdot BF $$

The “bifacial factor” $ BF $ is a database specification of the PV module. Typical values are between 0.7 and 0.8 (70 to 80 %). The factor indicates what percentage of the power incident on the back of the PV module can be used to generate electricity.

Calculation of backside radiation

For roof-parallel or façade-integrated systems

No radiation on the back side.

For vertical module rows

For elevation angles of more than 80°, the irradiation of the front and rear sides is calculated with the usual radiation models.

For elevated module rows

The radiation on the rear side of the module consists of the radiation reflected from the ground, the radiation reflected from adjacent modules and the proportion of diffuse and direct radiation that can directly reach the rear side of the module.

$$ E_\text{rear} = E_\text{rear,ground} + E_\text{rear,module} +E_\text{rear,diffuse} $$

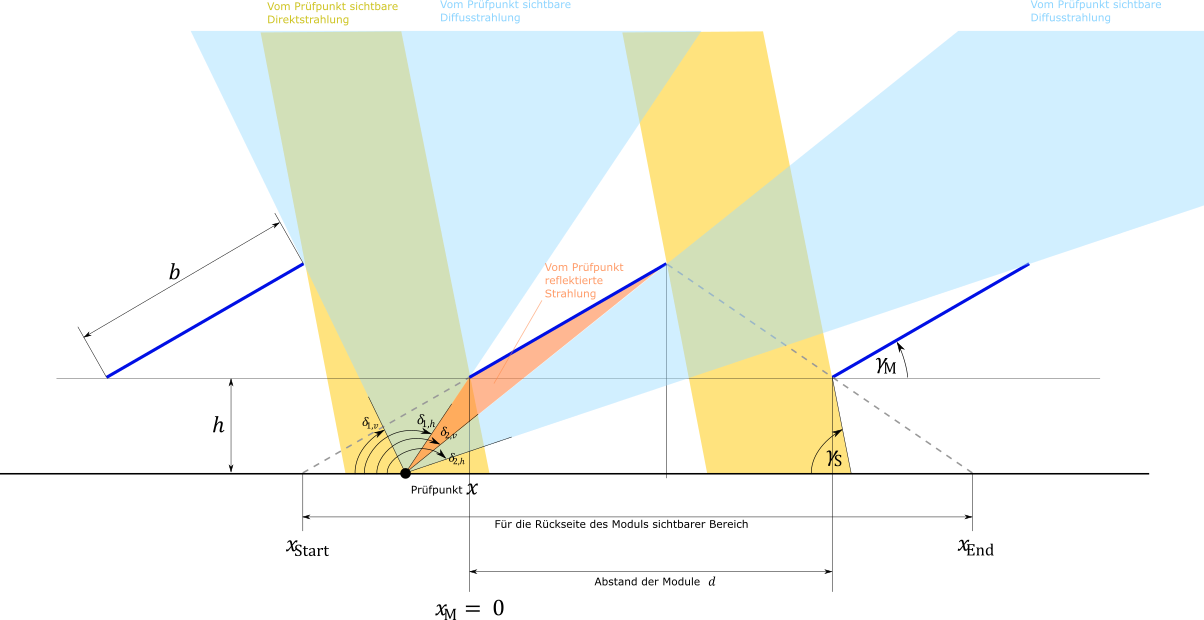
The area of the floor visible to the rear of the module starts at $$ x_\text{Start} = x_\text{M} - \frac{h}{\tan⁡ γ_\text{M}} $$ and ends at $$ x_\text{End} =x_\text{M} +d + \frac{ h(d-b \cos⁡ γ_\text{M})}{(b \sin⁡ γ_\text{M})} $$

with the module width b, the height above the ground h and the module distance d.

The incoming radiation is calculated for each point on the area of the ground visible to the module $$E_\text{In,test point} =E_\text{direct,test point} +E_\text{diffuse,test point} $$

The direct radiation reaches the test point in the following areas $$ [x_\text{M} + b \cos⁡ γ_\text{M} -d+ \frac{h+b \sin⁡ γ_\text{M}}{\tan⁡ γ_\text{S}} , x_\text{M} + \frac{ h}{\tan⁡ γ_\text{S}} ] $$ and $$ [x_\text{M} + b \cos⁡ γ_\text{M} +\frac{(h+b \sin⁡ γ_\text{M})}{\tan⁡ γ_\text{S}} , x_\text{M} + d + \frac{h}{\tan γ_\text{S}} ] $$

The diffuse radiation reaches the test point in proportion to the visible area of the sky. From the test point, two areas of the sky are visible, between the predecessor module and the module, and between the module and the successor module.

The front boundary of the front area runs between the test point and the top edge of the predecessor module. $$ \tan⁡ δ_\text{(1,v)} = \frac{h+b \sin γ_\text{M}}{b \cos γ_\text{M} -d-x} $$ The rear boundary of the front area runs between the test point and the lower edge of the module. $$ \tan⁡ δ_\text{(1,h)} = \frac{h}{x} $$ The front boundary of the rear area runs between the test point and the upper edge of the module. $$ \tan⁡ δ_\text{(2,v)} = \frac{h+b \sin⁡ γ_\text{M}}{x+b \cos⁡ γ_\text{M} } $$ The rear boundary of the rear area runs between the test point and the lower edge of the successor module. $$ \tan⁡ δ_\text{(2,h)} = \frac{h}{x+d} $$

The diffuse radiation at the test point then results in

$$ E_\text{diffuse,test point} = E_\text{diffuse} \frac{(δ_\text{(1,h)}-δ_\text{(1,v)} )+(δ_\text{(2,h)}-δ_\text{(2,v)} )}{180° } $$

Depending on the Albedo ρ a part of the radiation reaching the test point is reflected: $$ E_\text{Out,test point} = ρ \cdot E_\text{In,test point} $$

Of this radiation assumed to be isotropic, only a part reaches the rear side of the module, which still is weighted by the irradiation angle $ θ_\text{rear,test point} $: $$ E_\text{Out,test point,module} = E_\text{Out,test point} \frac{ δ_\text{(1,h)}-δ_\text{(2,v)}}{180° } \cdot IAM \cdot θ_\text{rear,test point} \cdot (1-f_\text{Shading by structure} ) $$

The mean angle of incidence is approximated by

$$ θ_\text{rear,test point} = \frac{δ_\text{(1,h)}+δ_\text{(2,v)}}{2} - γ_\text{M} $$

The calculation is repeated for $ n $ test points between $ x_\text{Start} $ and $ x_\text{End} $, whereby each irradiation on the test point is weighted with $ (x_\text{End} - x_\text{Start} )/n $. Afterwards it is integrated over all $ E_\text{Out,test point,module} $ and one receives the radiation reflected from the ground on the module rear side.

$$ E_\text{rear,ground} = \sum_{i=0}^{n} E_\text{Out,test point,module, i} (x_\text{End} - x_\text{Start} )/n $$

$ E_\text{rear,diffuse} $ corresponds to the proportion of diffuse radiation visible from the back of the module.

$$ E_\text{rear,diffuse} =E_\text{diffuse} \frac{γ_\text{M} -γ_\text{M,next} }{180°} $$

The angle from the lower edge of the module to the upper edge of the next module $ γ_\text{M,next} $ is calculated as follows $$ \tan⁡γ_\text{M,next} = \frac{b \sin⁡ γ_\text{M}}{d+b \cos⁡ γ_\text{M} } $$

See also

• Pages > PV modules > Bifacial modules